目次
令和2年度技術士第一次試験問題解答(機械)03
令和2年度技術士第一次試験問題解答(機械)03
【正答番号:⑤】
【正答番号:⑤】
<この内容の解説者>

【経歴】元軸受メーカー技術者。現在は、自動車部品メーカー技術者。技術士一次試験(機械)合格。
【専門】軸受、材料力学、金属材料(熱処理)
<問題>
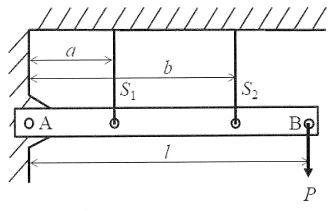
下図に示すように,剛体棒ABが滑節な節点Aで剛体壁に固定され,さらに2本の同一な鋼線で天井から水平に支えられている。B点に下向きに荷重Pを負荷したとき, これら鋼線に生じる引張力S1, S2の組合せとして,最も適切なものはどれか。
①\(S_1=\frac{l-b}{a-b}P\), \(S_2=\frac{l-a}{a-b}P\)
②\(S_1=\frac{l+b}{a-b}P\), \(S_2=\frac{l+a}{a-b}P\)
③\(S_1=\frac{a}{l}P\), \(S_2=\frac{b}{l}P\)
④\(S_1=\frac{al}{a^2-b^2}P\), \(S_2=\frac{bl}{a^2-b^2}P\)
⑤\(S_1=\frac{al}{a^2+b^2}P\), \(S_2=\frac{bl}{a^2+b^2}P\)
【正答番号:⑤】
出典元: 公益社団法人日本技術士会
解説
材料力学の問題です。まず、問題文から下記の情報が読み取れます。
・剛体棒・・・変形しない
・同一な鋼線・・・断面積や強度が同一
・滑節なAB・・・ピン支持。平行移動は拘束+回転フリー
あと、伸びの公式を思い出しておきましょう。式の導出は令和2年度技術士第一次試験問題解答(機械)02を参照してください。
\(\lambda=L_0\varepsilon=\frac{PL_0}{AE}\)
<モーメントつり合い>
A点まわりのモーメントのつり合いを考えると①式ができます。
\(S_1a+S_2b=Pl\)・・・①
<鋼線の伸び>
鋼線は、剛体ではないため伸びます。荷重Pが負荷されると下図のようにたわみ(伸び)λが生じる。
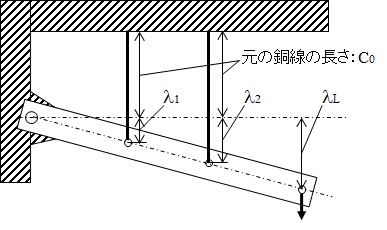
伸びはA点からの長さに比例する。
\( \lambda_1: \lambda_L=a:l\)
\( \lambda_1=\frac{a}{l}\lambda_L \)
\( \lambda_2: \lambda_L=b:l\)
\( \lambda_2=\frac{b}{l}\lambda_L \)
\(\frac{\lambda_1}{\lambda_2}=\frac{a}{l}\lambda_L\div\frac{b}{l}\lambda_L =\frac{a}{b}\)・・・②
\(\lambda_1\)・・・a位置の鋼線の伸び
\(\lambda_2\)・・・b位置の鋼線の伸び
\(\lambda_L\)・・・l位置の鋼線の伸び
同一な鋼線なので、引張力S1, S2が生じる銅線の長さ、断面積、縦弾性係数は同一。各記号は下記とする。
C・・・鋼線の長さ
A・・・鋼線の断面積
E・・・鋼線の縦弾性係数
伸びの式より、a位置とb位置の鋼線の伸びは、
\(\lambda_1=\frac{S_1C}{AE}\), \(\lambda_2=\frac{S_2C}{AE}\)
\(\frac{\lambda_1}{\lambda_2}=\frac{S_1}{S_2}\)・・・③
②、③式より
\(\frac{\lambda_1}{\lambda_2}=\frac{S_1}{S_2}=\frac{a}{b}\)
\(S_1=\frac{a}{b}S_2\)・・・④
①式に④式を代入
\(\left(\frac{a}{b}S_2\right)a+S_2b=Pl\)
\(S_2\left(\frac{a^2}{b}+b\right)=Pl\)
\(S_2\left(\frac{a^2+b^2}{b}\right)=Pl\)
\(S_2=\frac{bl}{a^2+b^2}P\)・・・⑤
④式に⑤式を代入
\(S_1=\frac{a}{b}S_2=\frac{a}{b}\times\frac{bl}{a^2+b^2}P=\frac{al}{a^2+b^2}P\)
よって、正解は「⑤」です。
この問題で問われていることは?
この問題で問われていることは?
剛体棒のモーメントつり合いを理解しているか。
3D-CADを用いて、FEMができるようになっていますが、どこにどれくらいの力が働くか推測できないと解析ができません。
FEMの荷重条件や拘束条件の設定を不十分だと、間違った結果しかでてきません。
今後は、今まで以上にFEMの必要性が増すはずなので、しっかり勉強しておきましょう。