目次
令和2年度技術士第一次試験問題解答(機械)02
令和2年度技術士第一次試験問題解答(機械)02
【正答番号:⑤】
【正答番号:⑤】
<この内容の解説者>

【経歴】元軸受メーカー技術者。現在は、自動車部品メーカー技術者。技術士一次試験(機械)合格。
【専門】軸受、材料力学、金属材料(熱処理)
<問題>
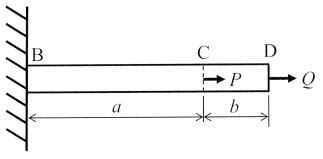
下図に示すように, 長さa+b, 断面積 A,縦弾性係数Eの一様断面な棒がある. その棒は,左端Bで剛体壁に固定されている. 棒のC点及びD点にそれぞれ軸力 P, Q を作用させたとき,棒全体の伸びとして,最も適切なものはどれか。
①\(\frac{Pa+Qb}{AE}\)
②\(\frac{P(a-b)+Qb}{AE}\)
③\(\frac{P(a-b)+Q(a+b)}{AE}\)
④\(\frac{P(a+b)+Q(a-b)}{AE}\)
⑤\(\frac{Pa+Q(a+b)}{AE}\)
【正答番号:⑤】
出典元: 公益社団法人日本技術士会
解説
材料力学の問題です。まず、下記の公式を思い出しましょう。
\(応力\sigma=\frac{P}{A}\)・・・①
P・・・荷重
A・・・断面積
\(ひずみ\varepsilon=\frac{L_1-L_0}{L_0}=\frac{\lambda}{L_0}\)・・・②
\(\lambda\)・・・伸び
\(L_0\)・・・初期の長さ
\(L_1\)・・・荷重が負荷された後の長さ
\(応力\sigma=\frac{E}{\varepsilon}\)・・・③
E・・・縦弾性係数(ヤング率)
今回の問題は、棒の伸びについての問いです。
伸び\(\lambda\)は、上記①~③式より下記の通り変換できます。
①、③式より、
\(\varepsilon=\frac{\sigma}{E}=\frac{P}{AE}\)・・・④
②、④式より
\(\lambda=L_0\varepsilon=\frac{PL_0}{AE}\)・・・⑤
では、本題に入りましょう。
C点とD点に軸力が作用しているので、分けて計算しましょう。
【C点の伸び】
問題文から下記が読み取れます。
軸力:P
長さ:a
断面積:A
縦弾性係数:E
上記よりC点の伸び\(\lambda_C\)は、⑤式より
\(\lambda_C=\frac{Pa}{AE}\)
【D点の伸び】
問題文から下記が読み取れます。
軸力:Q
長さ:a+b
断面積:A
縦弾性係数:E
上記よりC点の伸び\(\lambda_D\)は、⑤式より
\(\lambda_D=\frac{Q(a+b)}{AE}\)
【棒全体の伸び】
棒全体の伸び\(\lambda\)は、C点とD点の伸びの合計なので、
\(\lambda=\lambda_C+\lambda_D=\frac{Pa}{AE}+\frac{Q(a+b)}{AE}\)
\(\lambda=\frac{Pa+Q(a+b)}{AE}\)
よって、正解は「⑤」です。
この問題で問われていることは?
この問題で問われていることは?
荷重・応力・ひずみの関係を理解しているか。
開発品を試験する時、荷重とひずみなら測定できることがあります。供試体にひずみゲージを貼り、ひずみを測定することで応力を算出することができます。
求めた応力により、供試体の強度確認ができるようになります。